PCA is widely known by its geometric interpretation. That is, finding successive orthonormal vectors to project the data onto, such that the reprojected variance is kept at a maximum. Here is another way to look at PCA. Let’s say you have a data matrix $M$. You believe that there exists a low-rank matrix $L$—whose rank is less than $r$—if some noise is stripped out of $M$.

This can be formulated as an optimization problem, where you try to find a matrix $L$ that gives you the best low-rank approximation of $M$.

$$ \begin{align} & \min_{L} & & |M -L|_F^2 \
& \text{subject to} & & rank(L) < r \
\end{align} $$

Note that low-rank translates into the fact that there are correlations among samples and/or features. This ties our story back to the geometric interpretation of PCA. The solution to this problem is outliend by the famous Eckart-Young-Mirsky theorem, and is well-implemented in commonly used machine learning packages such as scikit-learn. It’s easy to solve whether you use SVD, as the original thorem suggests, or solving the eigenproblem of the covariance matrix of the data.

Something we haven’t talked about yet is the term $\|M -L\|_F^2$ . Why Frobenius norm? This basically represents your assumption on the noise that is present in your data $M$ or how do you like to penalize it. If you are like me and prefer the probabilistic view of PCA, this means that you assume your data is corrupted with i.i.d. Gaussian noise.

But what if it wasn’t?

Candes et al. raise this question in their 2011 paper. In their own words, if the data is grossly corrupted in sparse regions, then $\|M-L\|_F^2$ is not an appropriate objective anymore. Okay then, how about we change it to $\|M -L\|_1$? On paper, this seems perfect but we don’t have the Eckart-Young-Mirsky theorem for this case. Let’s take a step forward and don’t make any assumptions on what rank $r$ will be, but rather just try to minimize it as much as we can. While doing so, let’s also make sure a high-fidelity low-rank approximation via minimizing $\|S\|_1$which represents entry-wise deviations from the actual data. Obviously these two objectives are in a tradeoff, so we will represent our preference in between the two via a regularizing parameter $\lambda$. Here is the new objective function.

$$\begin{align}
& \min_{L} & & rank(L) + \lambda|S|_1 \
& \text{subject to} & & L + S = M \
\end{align}$$

Rank minimization over a convex set is an NP-hard problem therefore it’s not practical. What Candes et al. suggests is to replace $rank(L)$ with $|L|_*$ which is the nuclear norm of $L$. Nuclear norm is the convex envelope for the rank minimization problem, thus the bext convex approximation. In order to see why this is, let’s first formally define rank of a matrix as $rank(L) = |\sigma(L)|_0$, where $\sigma(L)$ is the vector of singular values of $L$. A refresher: the 0-“norm” (in quotation marks because it’s not really a norm) is simply the number of non-zero elements in a vector.

Nuclear norm uses the 1-norm, which is the tightest convex relaxation of the 0-“norm”, $|L|_* = |\sigma(L)|_1$. It is very useful in practice, and as we’ll see in other posts, opens up a plethora of applications where the eventual goal is to find a low-rank approximation of the data at hand.

Consequently, our minimaztion problem becomes a convex optimization problem:

$$\begin{equation*} \begin{aligned}
& \min_{L} & & |L|_* + \lambda|S|_1 \ & \text{subject to} & & L + S = M \\end{aligned}\end{equation*}$$

This problem defines what we call today, robust PCA. It can be solved efficiently via Alternating Direction Method of Multipliers (ADMM).

We saved the best question to the last: why would you want to use robust PCA for? While there are many applications one can think of, I find background-foreground separation in video surveillance to be the easiest to imagine. If frames captured by our camera is stored in a matrix $M$ (frames by pixels), then $L$ is the medium the camera looks at, background. It is low-rank since over many frames, the background stays the same and thus we have correlation among frames (also possibly among pixels as it is common in images). Sparse errors $S$ then becomes moving objects, or the foreground.

Robust PCA in Action

I grabbed the first few seconds following royalty free airport camera footage from YouTube.

It fits my definition above, since the camera is fixed at a location and it doesn’t rotate around. There are a few sparse objects moving around.

By applying robust PCA, I could easily separate background from the moving object (in this case, the truck and a couple of planes to the very right of the frame through the end of the video).

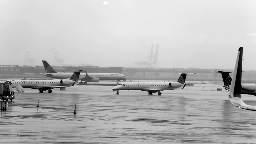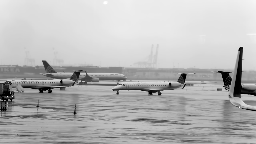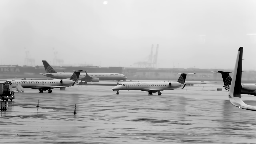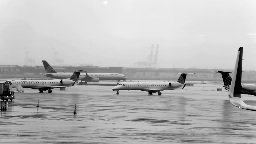
Had we have done it with PCA? Well…

I guess it’s good for making viral ghost footage videos.